Shape Analysis With Hyperbolic Wasserstein Distance
Jie Shi, Wen Zhang, Yalin Wang
Abstract
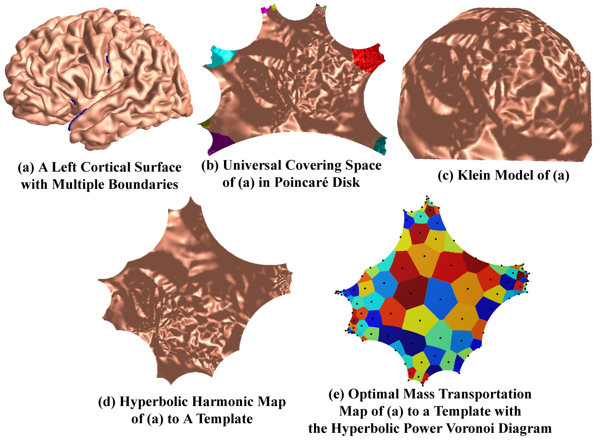
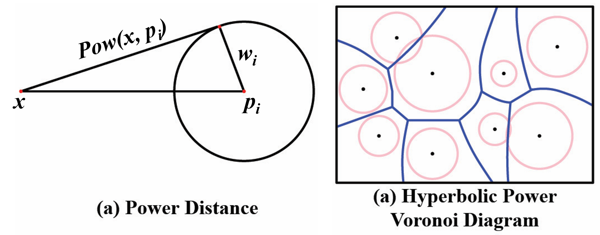
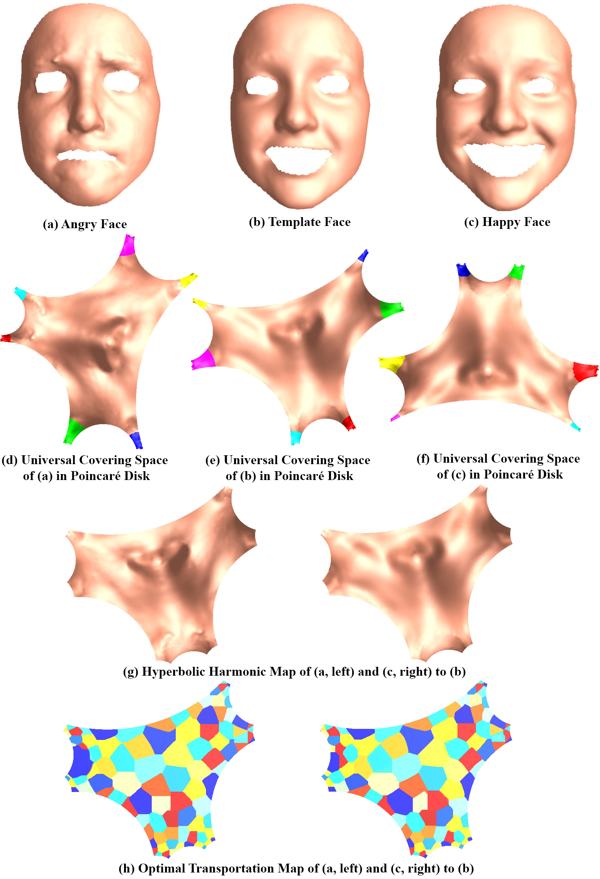
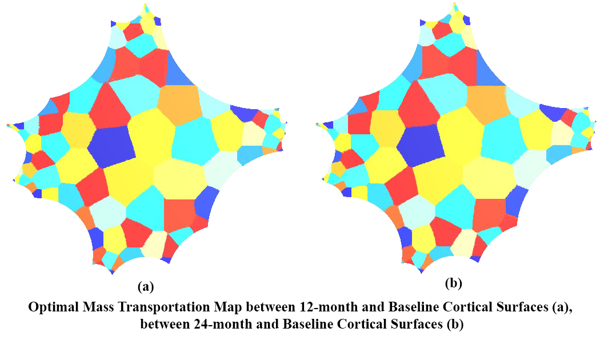
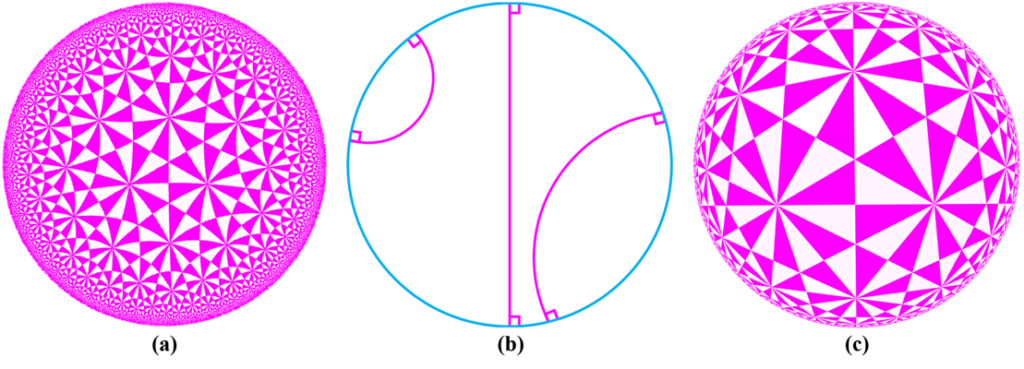
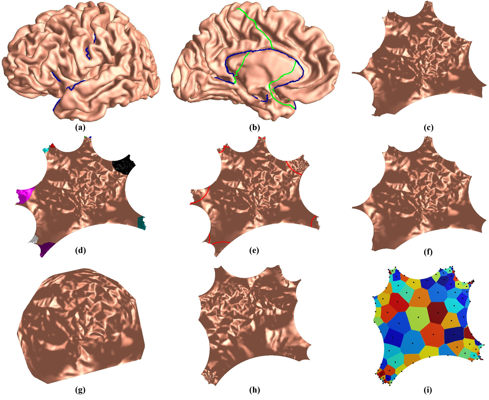
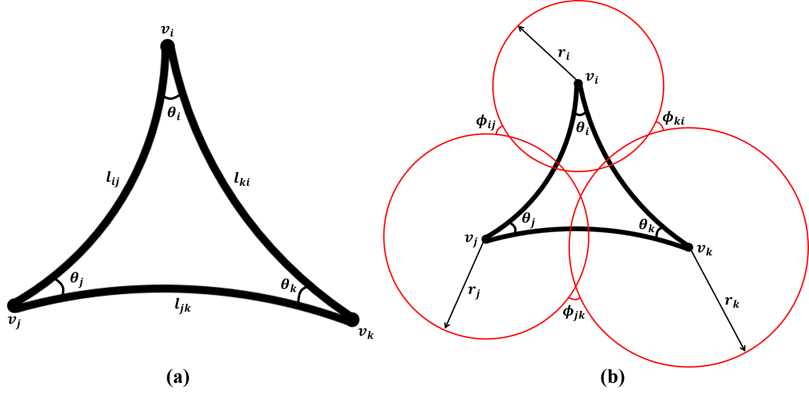
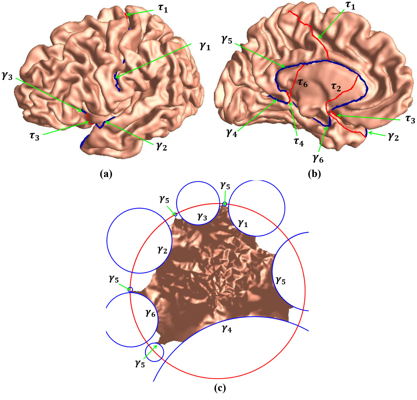
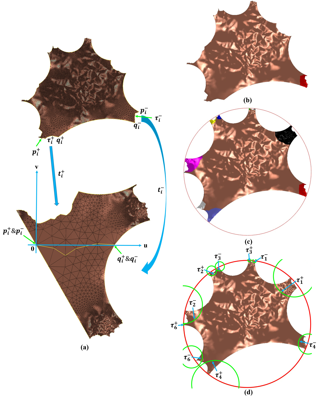
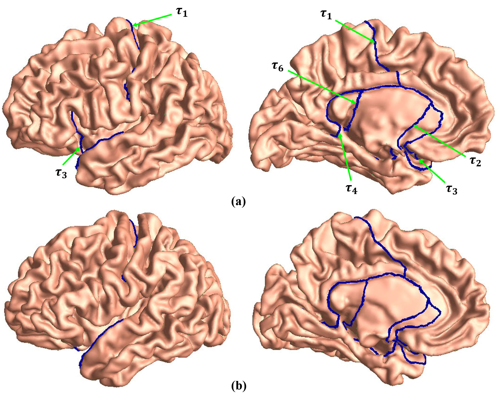
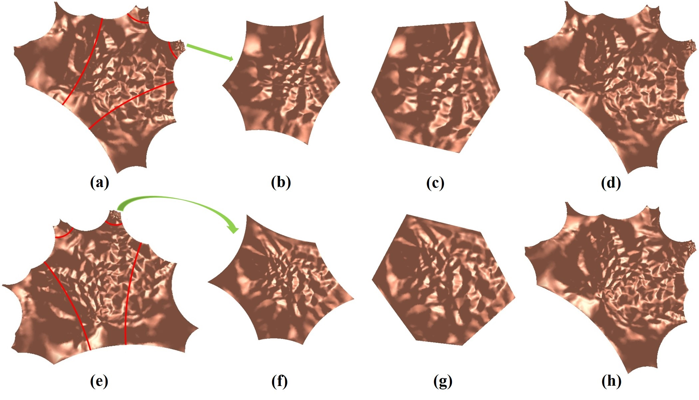
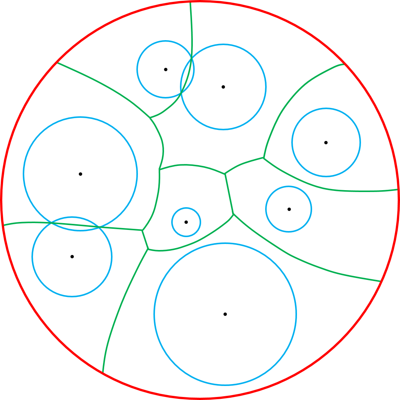
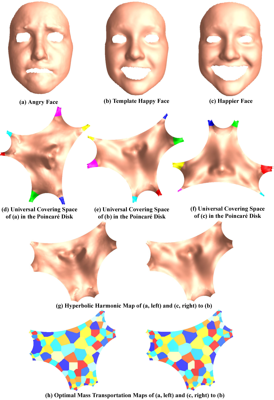
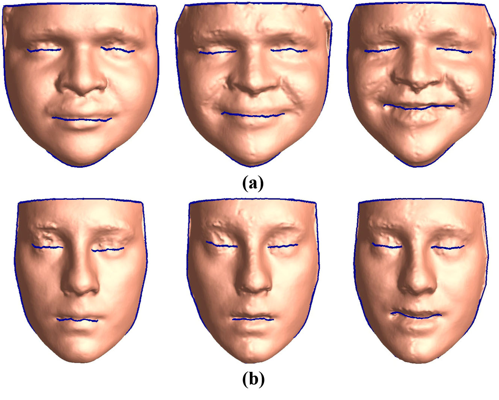
Shape space is an active research field in computer vision study. The shape distance defined in a shape space may provide a simple and refined index to represent a unique shape. Wasserstein distance defines a Riemannian metric for the Wasserstein space. It intrinsically measures the similarities between shapes and is robust to image noise. Thus it has the potential for the 3D shape indexing and classification research. While the algorithms for computing Wasserstein distance have been extensively studied, most of them only work for genus-0 surfaces. This paper proposes a novel framework to compute Wasserstein distance between general topological surfaces with hyperbolic metric. The computational algorithms are based on Ricci flow, hyperbolic harmonic map, and hyperbolic power Voronoi diagram and the method is general and robust. We apply our method to study human facial expression, longitudinal brain cortical morphometry with normal aging, and cortical shape classification in Alzheimer’s disease (AD). Experimental results demonstrate that our method may be used as an effective shape index, which outperforms some other standard shape measures in our AD versus healthy control classification study.
Figures (click on each for a larger version):
Hyperbolic Wasserstein Distance for Shape Indexing
Jie Shi, Yalin Wang
Abstract
Shape space is an active research topic in computer vision and medical imaging fields. The distance defined in a shape space may provide a simple and refined index to represent a unique shape. This work studies the Wasserstein space and proposes a novel framework to compute the Wasserstein distance between general topological surfaces by integrating hyperbolic Ricci flow, hyperbolic harmonic map, and hyperbolic power Voronoi diagram algorithms. The resulting hyperbolic Wasserstein distance can intrinsically measure the similarity between general topological surfaces. Our proposed algorithms are theoretically rigorous and practically efficient. It has the potential to be a powerful tool for 3D shape indexing research. We tested our algorithm with human face classification and Alzheimer’s disease (AD) progression tracking studies. Experimental results demonstrated that our work may provide a succinct and effective shape index.
Figures (click on each for a larger version):
Related Publications
- Jie Shi, Yalin Wang, Hyperbolic Wasserstein Distance for Shape Indexing, IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 2019, pp. TBD
- Jie Shi, Wen Zhang, Yalin Wang, Shape Analysis With Hyperbolic Wasserstein Distance, The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 5051-5061
- Mi Liang, Zhang Wen, Zhang J, Fan Y, Goradia D, Chen K, Reiman EM, Gu X, Wang Y, An Optimal Transportation based Univariate Neuroimaging Index, IEEE International Conference on Computer Vision (ICCV), 2017
- Zhang W, Shi J, Yu J, Zhan L, Thompson PM, Wang Y , Enhancing Diffusion MRI Measures by Integrating Grey and White Matter Morphometry with Hyperbolic Wasserstein Distance, IEEE International Symposium on BIOMEDICAL IMAGING: From Nano to Macro (ISBI). 2017