Multimodal-Longitudinal-Brain-Network-Coupling
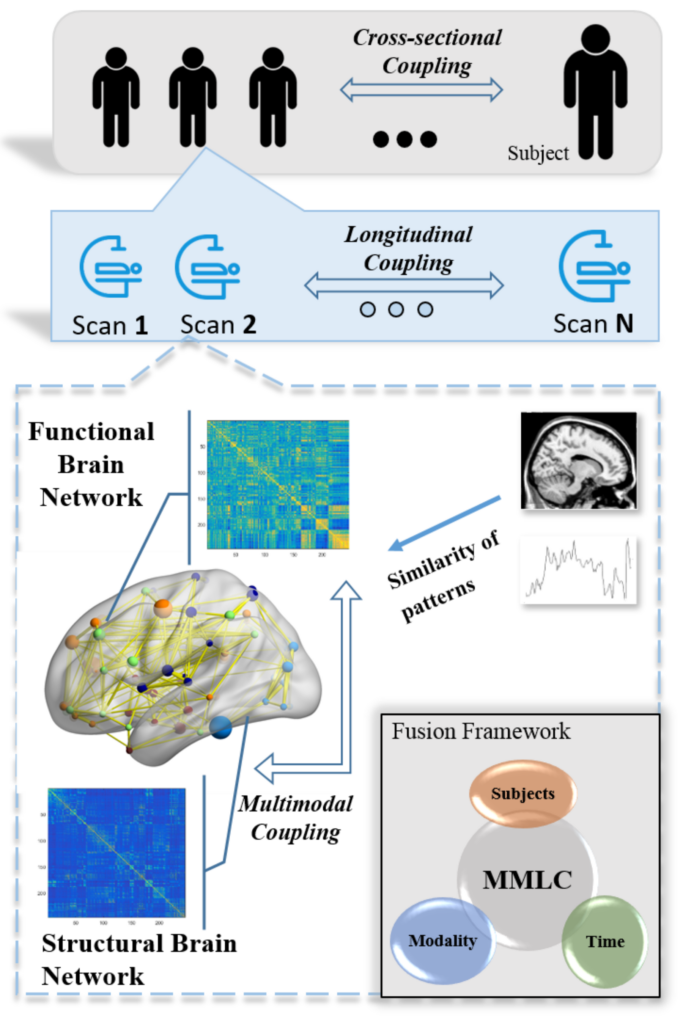
In recent years, brain network analysis has attracted considerable interests in the field of neuroimaging analysis. It plays a vital role in understanding biologically fundamental mechanisms of human brains. As the upward trend of multi-source in neuroimaging data collection, effective learning from the different types of data sources, e.g. multimodal and longitudinal data, is much in demand. In this paper, we propose a general coupling framework, the multimodal neuroimaging network fusion with longitudinal couplings (MMLC), to learn the latent representations of brain networks. Specifically, we jointly factorize multimodal networks, assuming a linear relationship to couple network variance across time. Experimental results on two large datasets demonstrate the effectiveness of the proposed framework. The new approach integrates information from longitudinal, multimodal neuroimaging data and boosts statistical power to predict psychometric evaluation measures.
System Setting
Add the four functions (.m files) in the Code.ZIP to the local environment of MATLAB R2017(or above version) and follow the instruction in MFCoupling.m for configuration.
Running Code
Run MFCoupling in MFCouping.m as:
[U, Vf, Vd, Vfc, Vdc, Loss] = MFCoupling(R_train, K, lambda, lr, maxiter)
The optimization details can be found in Alg.1 in the paper.
Inputs:
R-train: Network data. A matrix with 5 dimensions in order N*N*Nuser*Ntime*Nmod. N is the number of nodes predefined in brain networks, Nuser is the number of subjects, Ntime is the number of scans, Nmod is the number of modalities. Here, Ntime=3 and Nmod = 2.
K: a scalar hyperparameter for the dimension of the latent space.
lambda (struct type): Contains 4 scalar hyperparameters, lambda.lb1~4.
lambda.lb1: as alpha in Eq.9 (Total loss);
lambda.lb2 = lambda.lb3: as lambda_1 in Eq.9. Please notice that functional and structural networks are not necessary to have the same loss weights.
lambda.lb4: as lambda_2 in Eq.9. It is the weight for the regularization term.
lr: Learning rate.
maxiter: max iteration of the training.
Outputs:
U: Coeeficient matrix. A 4-dimensional matrix. N*K*Nuser*Ntime.
Vf and Vd: The representation matrix of functional networks (Vf) and structural networks (Vd). Each matrix has the dimension N*K*Nuser*Ntime. Eventually, each subject has a new feature matrix [Vf, Vd] for the future classification/prediction experiments.
Vfc and Vdc: Group consistent matrix of the brain networks at each scan. Two 3-dimensional matrix, N*K*Ntime.
Any problem, please directly contact Wen Zhang, at wenzhang.ccm at gmail.com.