Multi-Resemblance Multi-Target Low-Rank Coding (MMLC)
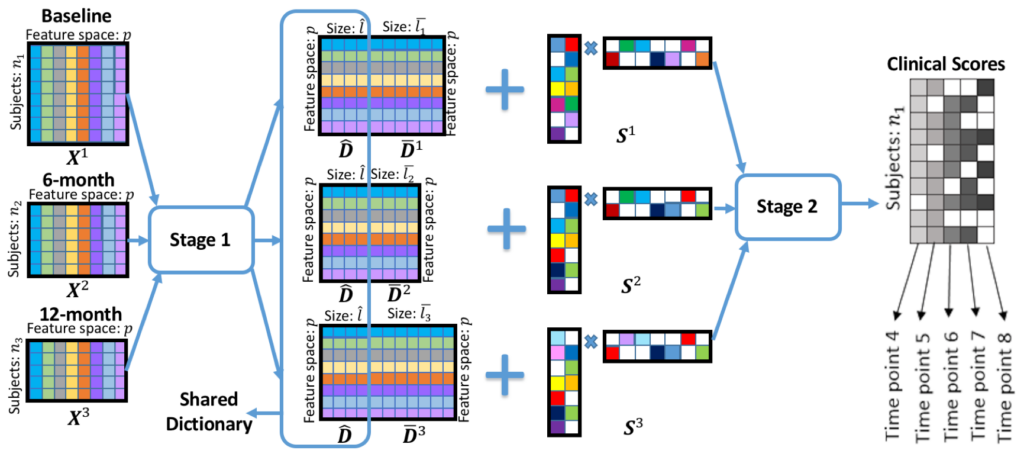
Alzheimer’s Disease (AD) is the most common type of dementia. Identifying correct biomarkers may determine pre-symptomatic AD subjects and enable early intervention. Sparse coding (SC) has shown strong statistical power in many biomedical informatics and brain image analysis researches. However, the SC computation is time-consuming and often leads to inconsistent codes, i.e., local features with similar descriptors tend to have different sparse codes, and longitudinal analysis always contains incomplete data and missing label information. To address above challenges, we invent a novel two-stage Multi-Resemblance Multi-Target Low-Rank Coding (MMLC), which encourages that sparse codes of neighboring time point longitudinal features to be resemblant to each other and only a few sparse codes are necessary to represent all features in a local region to reduce the computational cost. In stage one, we propose an online multi-resemblant low-rank SC method to utilize the common and task-specific dictionaries in different time points data to capture the multiple time points longitudinal correlation. In stage two, supported by rigorous theoretical analysis, we develop a multi-target learning method to solve the missing label problem. To solve such a multi-task sparse low-rank optimization problem, we propose a stochastic coordinate coding method with a sequence of closed-form update steps which reduce the computational cost guaranteed by a theoretical fast convergence proof.
Usage
Running Code
We implemented the algorithm as described in the paper-based on c++, Matlab and Python.
Run examples
In this code, you can run our algorithm on the test dataset. If you want to use our surface-based morphometry features (mTBM), please contact me to get access to the features.
If you execute our two-stage MMLC, you can reproduce our model.
Stage 1: Multi-Resemblant Low-rank Sparse Coding
Stage 2: Multi-Target Regression
Further MMLC Details
Setup
First follow the instructions for installing Matlab and g++.
This package requires Matlab 2012a+ and g++ 4.6+
Then, clone this repository using
$ git clone https://github.com/zj00377/MMLC
Sample data and preprocessing
If you want to use our MMS features in the paper, please contact the author of the paper to get access.
For other usages, please prepare your multi-task feature matrix into with M * N dimension. N is the number of samples and M is the dimension of each sample.
Please list your input information into Input_info.txt. Here is an example of four tasks as inputs. (You can check our sample matrices in this repo)
- sample1.txt 2204
- sample2.txt 2204
- sample3.txt 2204
- sample4.txt 2204
- sparseCode1.txt 1500
- sparseCode2.txt 1500
- sparseCode3.txt 1500
- sparseCode4.txt 1500
- D1.txt
- D2.txt
- D3.txt
- D4.txt
sample1.txt ~ sample4.txt are the feature matrices for four tasks and 2204 is N (the number of samples in each task), sampleDim = 400 (in run.cpp) is M (the dimension of input features) for each task. M can be different for different tasks. sparseCode1.txt ~ sparseCode4.txt are the sparse codes with dimension of K * N for four tasks and 1500 is K (the dimension of sparse codes). D1.txt ~ D4.txt are the dictionaries for four tasks which includes common and individual dictionaries, its dimension is M * K.
Learning multi-task dictionaries and sparse codes
g++ run.cpp -o run -O3
Once you finish one epoch and get the latest sparse codes, you can path all sparse codes matrices into the following functions
python lowRank_SCodes.py -i /input path/to/sparsecodes/txtfile -o /output path/to/sparsecodes/txtfile –lambda1 0.13 –lambda2 0.1 –lambda3 1000 -t 4
Then, you can use the sparsecodes%i_new.txt files as the initial sparse codes for the next epoch of run.cpp. Please repeat above procedure for 10 times.
**sparse feature K usually 5 times of input sample dimension M
You can modify the common dictionary size via change dictionarySize = 500 in run.cpp, the best performance is achieved by 1:1 split the common and individual dictionary in our paper.
Max-pooling
./MaxPooling featureDim batchSize FeatureFileName outputFile
FeatureFileName = ‘sparseCode1.txt’ (the name of the output from MMLC stage1) featureDim is M (the dimension of sparse codes) batchSize is the number of patches for each subject outputFile = ‘Feature1.txt’ (the name of the features which we will use do the prediction)
Here is the example
./MaxPooling 1500 4 SparseCode1.txt Feature1.txt
./MaxPooling 1500 4 SparseCode1.txt Feature1.txt
Running the regression stage
Run the example code using
$ [ predict, testclass, rMSE] = regression(AD, MCI, CU, ratio, sample, label, Method)
AD = the number of subjects of AD MCI = the number of subjects of MCI CU = the number of subjects of normal control ratio = the ratio for split training and testing set, default is 0.9 sample = feature matrix for all subjects, which is the output of max-pooling by stage 1 of MMLC label = the ground truth for all subjects, here is MMSE or ADAS value. Method = ‘Lasso’ or ‘Ridge’ regression
Here is an example of running stage 2.
[ predict, testclass, rMSE] = regression(194, 388, 224, 0.9, ‘Feature1.txt’, MMSE, ‘Lasso’)
The outputs are the predict MMSE or ADAS value (predict) with the ground truth (testclass) and the rMSE value. And the script will output as follows:
rMSE 2.24
Authors
Jie Zhang [email protected]
Yalin Wang [email protected]