Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative

Yonghui Fan, Gang Wang, Qunxi Dong, Yuxiang Liu, Natasha Lepore, Yalin Wang

Abstract

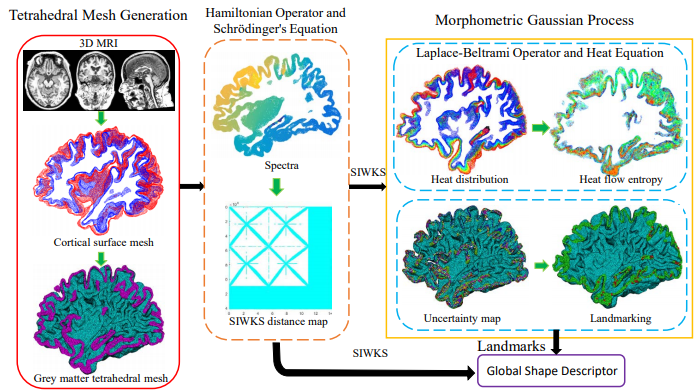
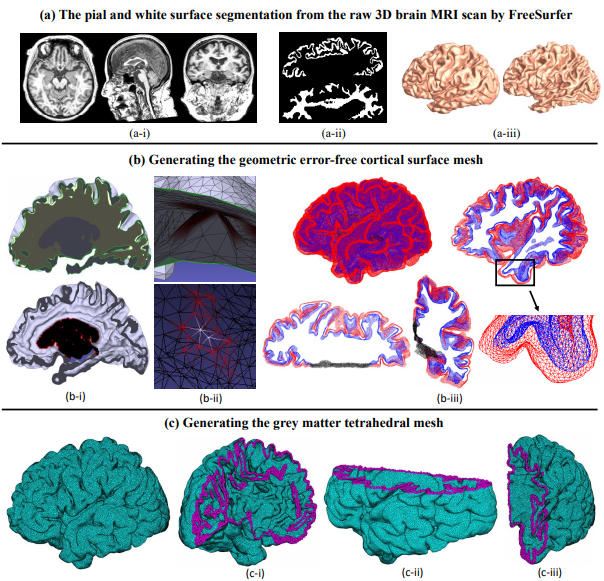
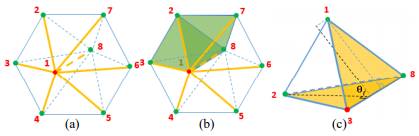
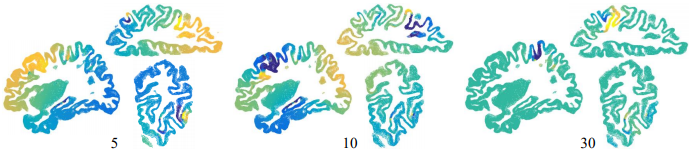
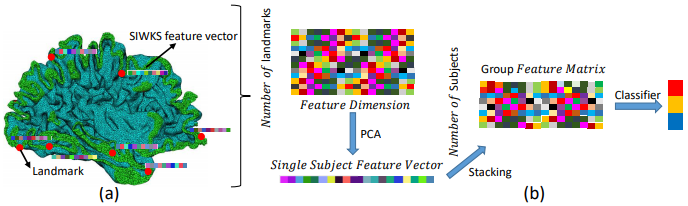
Structural and anatomical analyses of magnetic resonance imaging (MRI) data often require a reconstruction of the three-dimensional anatomy to a statistical shape model. Our prior work demonstrated the usefulness of tetrahedral spectral features for grey matter morphometry. However, most of the current methods provide a large number of descriptive shape features but lack an unsupervised scheme to automatically extract a concise set of features with clear biological interpretations and that also carries strong statistical power. Here we introduce a new tetrahedral spectral feature-based Bayesian manifold learning framework for effective statistical analysis of grey matter morphology. We start by solving the technical issue of generating tetrahedral meshes which preserve the details of the grey matter geometry. We then derive explicit weak-form tetrahedral discretizations of the Hamiltonian operator (HO) and the Laplace-Beltrami operator (LBO). Next, Schr ̈odinger’s equation is solved for constructing the scale-invariant wave kernel signature (SIWKS) as the shape descriptor. By solving the heat equation and utilizing the SIWKS, we design a morphometric Gaussianprocess (M-GP) regression framework and an active learning strategy to select landmarks as concrete shape descriptors. We evaluate the proposed system on publicly available data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI), using subjects structural MRI covering the range from cognitively unimpaired (CU) to full-blown Alzheimer’s disease(AD). Our analyses suggest that the SIWKS and M-GP compare favorably with seven other baseline algorithms to obtain grey matter morphometry-based diagnoses. Our work may inspire more tetrahedral spectral feature-based Bayesian learning research in medical image analysis.

Figures (click on each for a larger version):

Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative
Image of Tetrahedral Spectral Feature-Based Bayesian Manifold Learning for Grey Matter Morphometry: Findings from the Alzheimer’s DiseaseNeuroimaging Initiative