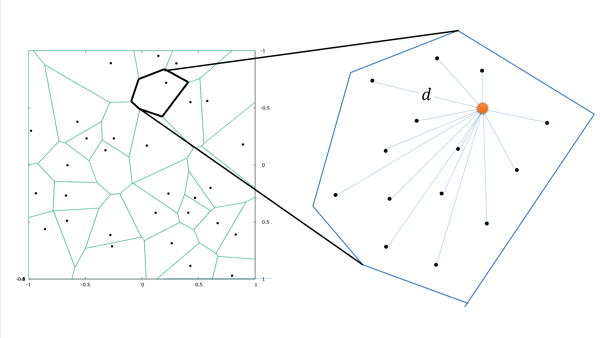
An Optimal Transportation based Univariate Neuroimaging Index

Mi Liang, Zhang Wen, Zhang J, Fan Y, Goradia D, Chen K, Reiman EM, Gu X, Wang Y

Abstract

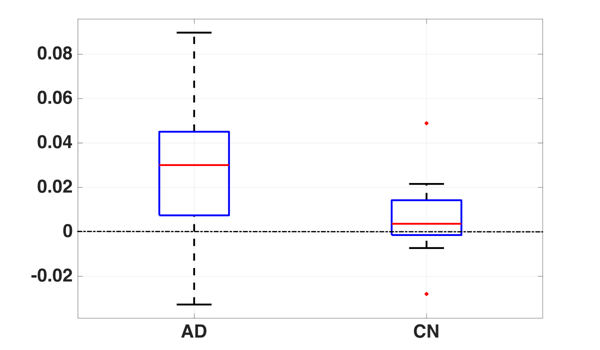
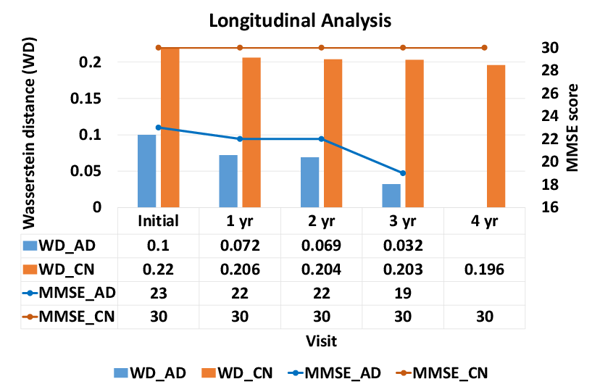
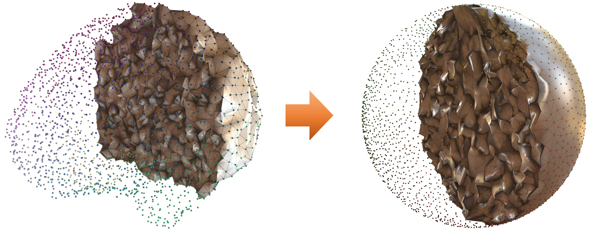
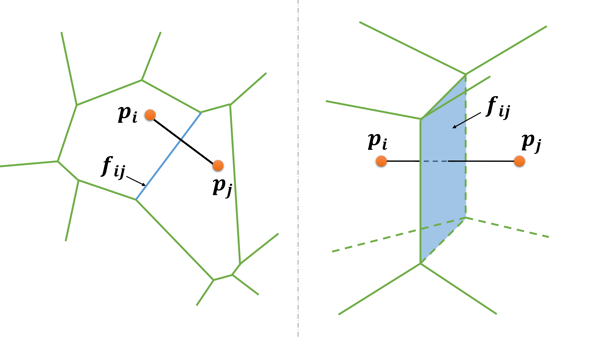
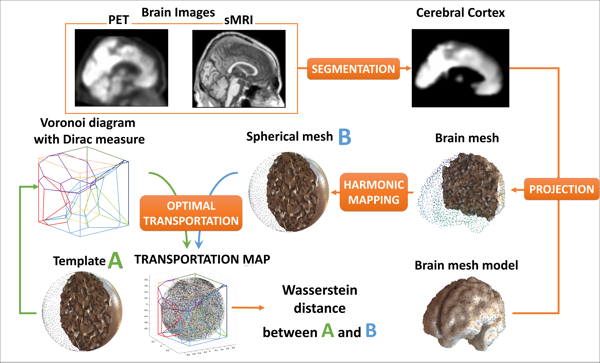
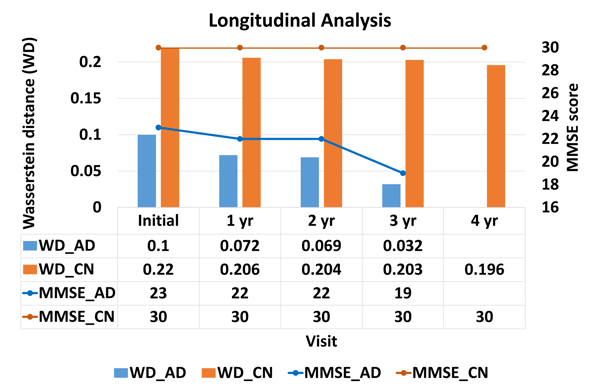
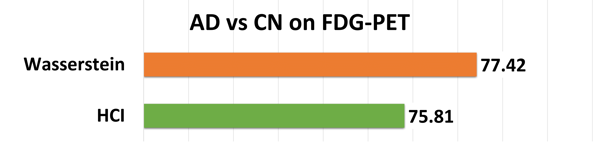
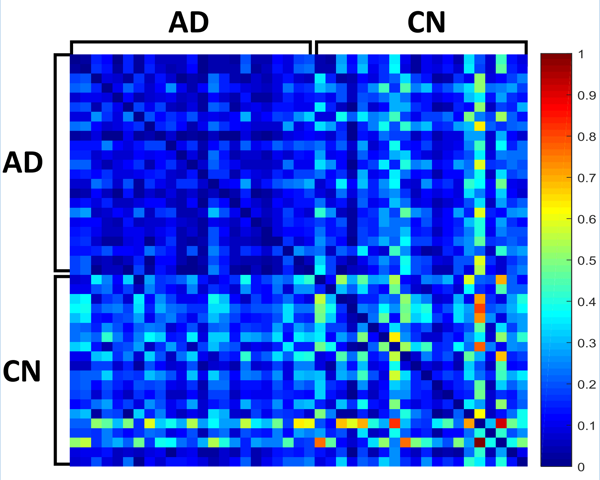
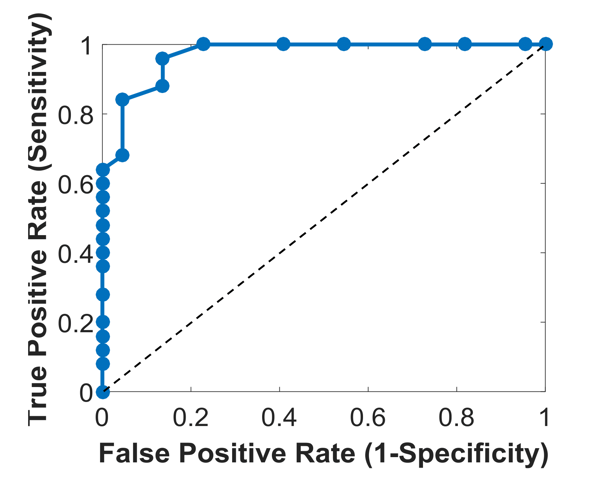
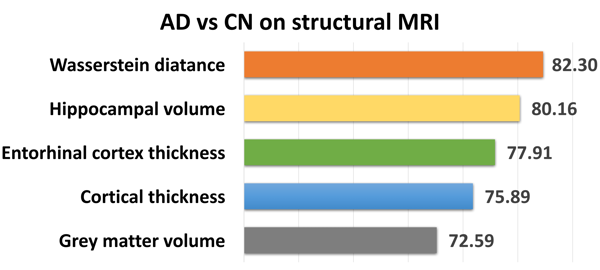
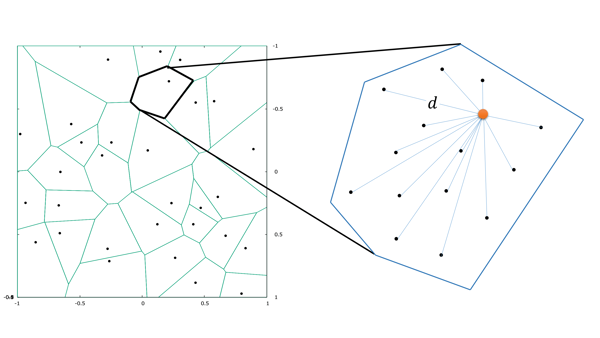
The alterations of brain structures and functions have been considered closely correlated to the change of cognitive performance due to neurodegenerative diseases such as Alzheimer’s disease and yet few univariate neuroimaging indices have been developed to quantify such alterations. The Wasserstein distance measures the similarity between two probability distributions on a given metric space. A brain image can be regarded as a 3D probability distribution, which provides the possibility to apply the Wasserstein distance to brain images in order to quantify the shape and function variance of human brains. In this paper, we propose a variational framework to compute the Wasserstein distance in 3D Euclidean space.\ignore{First, we convert a brain image into a tetrahedral mesh and harmonically map it to a unit sphere. After that, we use 3D power Voronoi diagram to compute the optimal transportation between the image and a template, which produces the Wasserstein distance between them.} We compute the pairwise Wasserstein distance between each image and a template. By comparing the distances from all the images to the common template, we obtain a concise and informative index for each image. Our framework makes use of the Newton’s method for solving the underlying optimal transportation problem, which reduces the computational cost and enables itself to be applicable to large-scale datasets. The proposed work is very general and may be applied to analyze various brain volumetric images, including structural magnetic resonance (sMR) and fluorodeoxyglucose positron emission tomography (FDG-PET) images. In the classification between Alzheimer’s disease patients and healthy controls, our method achieves an accuracy of $82.30\%$ on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) baseline sMRI dataset and outperforms several other indices. On FDG-PET dataset, we boost the accuracy to $88.37\%$ by leveraging groupwise Wasserstein distances. In a longitudinal study, we obtain a $5\%$ significance with $\var{p-value} = 1.13\times10^5$ in t-test on FDG-PET. The results demonstrate a great potential of the proposed index for neuroimage analysis and the precision medicine research.