A Tetrahedron-based Heat Flux Signature for Cortical Thickness Morphometry Analysis

Yonghui Fan , Gang Wang, Natasha Lepore, and Yalin Wang

Abstract

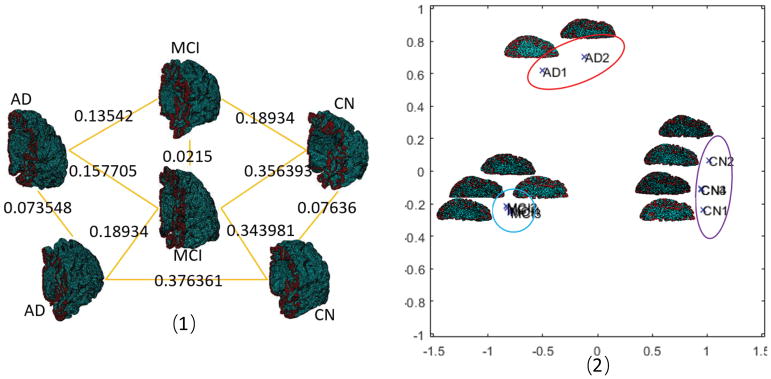
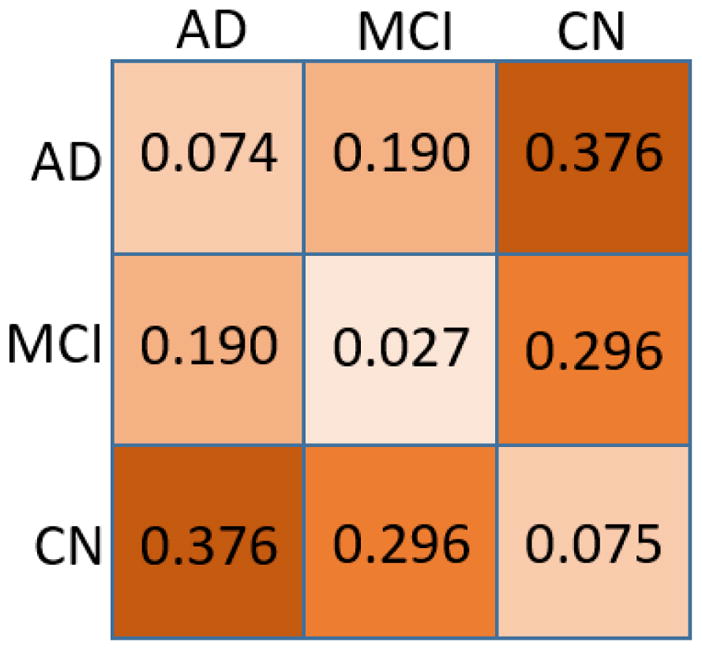
Cortical thickness analysis of brain magnetic resonance images is an important technique in neuroimaging research. There are two main computational paradigms, namely voxel-based and surfacebased methods. Recently, a tetrahedron-based volumetric morphometry (TBVM) approach involving proper discretization methods was proposed. The multi-scale and physics-based geometric features generated through such methods may yield stronger statistical power. However, several challenges, such as the lack of well-defined thickness statistics and the difficulty in filling tetrahedrons into the thin and curvy cortex structure, impede the broad application of TBVM. In this paper, we present a universal cortical thickness morphometry analysis approach called tetrahedron-based Heat Flux Signature (tHFS) to address these challenges. We define the tetrahedron-based weak form heat equation and Laplace-Beltrami eigen decomposition and give an explicit FEMbased discretization formulation to compute the tHFS. We further show a tHFS metric space with which cortical morphometric distances can be directly visualized. Additionally, we optimize the cortical tetrahedral mesh generation pipeline and fill dense high-quality tetrahedra in the grey matters without sacrificing data integrity. Compared with existing cortical thickness analysis approaches, our experimental results of distinguishing among Alzheimer’s disease (AD), cognitively normal (CN) and mild cognitive impairment (MCI) subjects shows that tHFS yields a more accurate representation of cortical thickness morphometry. The tHFS metric experiment provides a more vivid visualization of tHFS’s power in separating different clinical groups.

Figures (click on each for a larger version):

Related Publications